搜索和排序

搜索

线性搜索

Problem： Given an array arr[] of n elements, write a function to search a given element x in arr[].

Examples：

Input : arr[] = {10, 20, 80, 30, 60, 50, 
                     110, 100, 130, 170}
          x = 110;
Output : 6
Element x is present at index 6

Input : arr[] = {10, 20, 80, 30, 60, 50, 
                     110, 100, 130, 170}
           x = 175;
Output : -1
Element x is not present in arr[].

1
2
3
4
5
6
7
8
9
10
11

Implementation

/**
 * 线性搜索
 */ 
#include <stdio.h>

int search(int arr[], int n, int x)
{
    int i;
    for (i = 0; i < n; i++)
        if (arr[i] == x)
            return i;
    return -1;
}

int main(void)
{
    int arr[] = {2, 3, 4, 10, 20};
    int x = 10;
    int n = sizeof(arr) / sizeof(arr[0]);
    int result = search(arr, n, x);
    (result == -1) ? printf("Element is not present in array") : printf("Element is present at index %d", result);

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

时间复杂度是O(n)。

二分搜索

Problem：同上

Implementation

/**
 * 递归二分法搜索
 */
#include <stdio.h>

int binarySearch(int arr[], int l, int r, int x)
{
    if(r < l)
        return -1;

    int mid = l + (r - l) / 2;
    if(arr[mid] == x)
        return mid;
    if(arr[mid] > x)
        return binarySearch(arr, l, mid, x);
    return binarySearch(arr, mid, r, x);
}

int main(void)
{
    int arr[] = {2, 3, 4, 10, 40};
    int n = sizeof(arr) / sizeof(arr[0]);
    int x = 10;
    int result = binarySearch(arr, 0, n - 1, x);
    (result == -1) ? printf("Element is not present in array")
                   : printf("Element is present at index %d",
                            result);
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

/**
 * 迭代二分搜索
 */ 
#include <stdio.h>

int binarySearch(int arr[], int l, int r, int x)
{
    while(l <= r){
        int m = l + (r - l) / 2;
        if(arr[m] == x)
            return m;
        if(arr[m] < x)
            l = m + 1;
        else
            r = m + 1;
    }
    
    return -1;
}

int main(void)
{
    int arr[] = {2, 3, 4, 10, 40};
    int n = sizeof(arr) / sizeof(arr[0]);
    int x = 10;
    int result = binarySearch(arr, 0, n - 1, x);
    (result == -1) ? printf("Element is not present"
                            " in array")
                   : printf("Element is present at "
                            "index %d",
                            result);
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

跳跃搜索

和二分法搜索一样，跳跃搜索算法适用于已排序的数组。基础的想法就是通过跳过一些元素来比线性搜索少作一些比较。举例来说，假设我们有一个数组arr[]，大小为n，跳跃的步长为m，跳跃搜索先比较arr[0]， arr[m]， arr[2m]，..， arr[km]。如果找到了中间值(arr[km] < x < arr[km + m])，然后再进行线性搜索找到元素x。

那么最佳的步长是多少呢？在最坏的情况下，我们需要跳跃n/m次，然后检查这个值是不是大于我们要查找的元素，然后再进行m-1次的线性比较，总共的比较次数为 n/m + m - 1。当m = √n时这个值最小，因此最佳的步长为m = √n。

Implementation

/**
 * 跳跃搜索
 * 
 * gcc -lstdc++ -o d dump_search.cpp
 */

#include <cmath>
#include <iostream>

using namespace std;

int jumpSearch(int arr[], int x, int n)
{
    int step = sqrt(n);
    int index = 0;
    int max = 0;
    while(index < n)
    {
        if(arr[index] == x)
            return index;
        else if(arr[index] < x)
            index += step;
        else
            break;
    }

    max = index;
    index -= step;
    while(index < max)
    {
        if (arr[index] == x)
            return index;
        else
            index++;
    }
    return -1;
}

int main(int argc, char *argv[])
{
    int arr[] = {0, 1, 1, 2, 3, 5, 8, 13, 21,
                 34, 55, 89, 144, 233, 377, 610};
    int x = 0;
    if(argc == 2)
    {
        x = atoi(argv[1]);
    }

    int n = sizeof(arr) / sizeof(arr[0]);

    // 使用跳跃搜索查找x的索引
    int index = jumpSearch(arr, x, n);

    // 打印x的索引值
    cout << "\nNumber " << x << " is at index " << index;
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

插值搜索

线性搜索时间复杂度是O(n)，跳跃搜索为O(√n)，而二分法为O(Log n)。插值搜索(Interpolation Search)是二分法的一种改进算法，数组的元素值得是均匀分布的。二分搜索法总是从中间的元素开始搜索，而插值搜索法根据被查询的值可能会从不同的地方开始搜索。比如说如果键更靠近最后的元素，插值搜索就从后面开始查找。

通常使用下面的公式来确定查找的位置：

// 这个公式的主要思想是：当要查找的元素靠近更大的值arr[hi]时返回更大的索引值，
// 靠近更小的arr[lo]时返回小的索引值
// The idea of formula is to return higher value of pos
// when element to be searched is closer to arr[hi]. And
// smaller value when closer to arr[lo]

pos = lo + [ (x-arr[lo])*(hi-lo) / (arr[hi]-arr[Lo]) ]

arr[] ==> 待查找的数组
x     ==> 待查找的值
lo    ==> 开始查找的索引值
hi    ==> 结束查找的索引值

1
2
3
4
5
6
7
8
9
10
11
12

Implementation

/**
 * 插值搜索法
 */
#include <stdio.h>

int interpolationSearch(int arr[], int n, int x)
{
    int lo = 0, hi = n - 1;
    while(lo <= hi && x >= arr[lo] && x <= arr[hi])
    {
        if(lo == hi){
            if (arr[lo] == x)
                return lo;
            return -1;
        }
        int pos = lo + (((double)(hi - lo) / (arr[hi] - arr[lo])) * (x - arr[lo]));
        if(arr[pos] == x)
            return pos;
        if(arr[pos] < x)
            lo = pos + 1;
        else
            hi = pos - 1;
    }
    return -1;
}

int main()
{
    // Array of items on which search will
    // be conducted.
    int arr[] = {10, 12, 13, 16, 18, 19, 20, 21, 22, 23,
                 24, 33, 35, 42, 47};
    int n = sizeof(arr) / sizeof(arr[0]);

    int x = 18; // Element to be searched
    int index = interpolationSearch(arr, n, x);

    // If element was found
    if (index != -1)
        printf("Element found at index %d", index);
    else
        printf("Element not found.");
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

排序

选择排序

选择排序通过重复的从未排序数组中寻找最小的元素并将其放到最开始，维护着两个数组。流程如下：

arr[] = 64 25 12 22 11

// 在数组 arr[0...4] 中找到最小的元素 11，放到数组的最前面
11 25 12 22 64

// 在数组 arr[1...4] 中找到最小的元素 12，放到数组 arr[1...4] 的最前面 
11 12 25 22 64

// 在数组 arr[2...4] 中找到最小的元素 22，放到数组 arr[2...4] 的最前面 
11 12 22 25 64

// 在数组  arr[3...4]
// 中找到最小的元素 25，放到数组 arr[3...4] 的最前面 
11 12 22 25 64

1
2
3
4
5
6
7
8
9
10
11
12
13
14

Implementation

/**
 * 选择排序
 */

#include <stdio.h>

void swap(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void selectionSort(int arr[], int n)
{
    int i, j, m;
    for(i = 0; i < n - 1; i++){
        m = i;
        for(j = i + 1; j < n; j++)
            if(arr[j] < arr[m])
                m = j;
        swap(&arr[m], &arr[i]);
    }
}

void printArray(int arr[], int n)
{
    int i = 0;
    while(i<n){
        printf("%d\t", arr[i]);
        i++;
    }
    printf("\n");
}

int main()
{
    int arr[] = {64, 25, 12, 22, 11};
    int n = sizeof(arr) / sizeof(arr[0]);
    printArray(arr, n);
    selectionSort(arr, n);
    printf("Sorted array: ");
    printArray(arr, n);
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

冒泡排序

冒泡排序是最近的排序算法：重复的将临近的两个错误排序的元素交换。

Implementation

/**
 * 冒泡排序
 */ 
#include <stdio.h>

void swap(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void bubbleSort(int arr[], int n)
{
    int i, j;
    for(i = 0; i < n; i++)
    {
        for(j = 0; j < n - i - 1; j++)
        {
            if(arr[j] > arr[j+1])
                swap(&arr[j], &arr[j+1]);
        }
    }
}

void printArray(int arr[], int n)
{
    int i;
    for(i = 0; i < n; i++)
        printf("%d\t", arr[i]);
    printf("\n");
}

int main() 
{ 
    int arr[] = {64, 34, 25, 12, 22, 11, 90}; 
    int n = sizeof(arr)/sizeof(arr[0]); 
    bubbleSort(arr, n); 
    printf("Sorted array: \n"); 
    printArray(arr, n); 
    return 0; 
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

插入排序

原理如下：

插入排序

Implementation

/**
 * 插入排序
 */

#include <stdio.h>

void insertionSort(int arr[], int n)
{
    int i, key, j;
    for(i = 1; i < n; i++)
    {
        key = arr[i];
        for(j = i - 1; j >= 0; j--)
        {
            if(arr[j] > key)
                arr[j+1] = arr[j];
            else
                break;
        }
        arr[j+1] = key;
    }
}

void printArray(int arr[], int n)
{
    int i;
    for (i = 0; i < n; i++)
        printf("%d ", arr[i]);
    printf("\n");
}

int main() 
{ 
    int arr[] = { 12, 11, 13, 5, 6 }; 
    int n = sizeof(arr) / sizeof(arr[0]); 
  
    insertionSort(arr, n); 
    printArray(arr, n); 
  
    return 0; 
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

归并排序

和快速排序一样，归并排序是一种分而治之的算法。它将数组分成两半，再对这两半进行归并排序，最后合并这两半。

归并排序

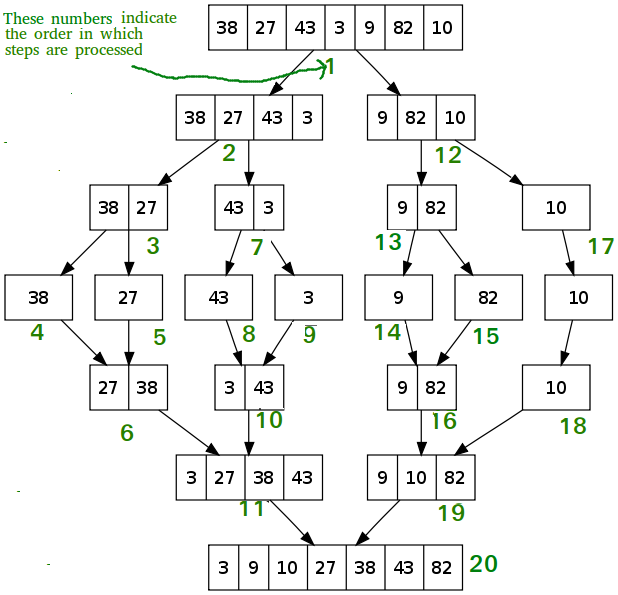
Implementation

/**
 * 归并排序
 */ 

#include <stdio.h>
#include <stdlib.h>

void merge(int arr[], int l, int m, int r)
{
    int i, j, k;

    int n1 = m - l + 1;
    int n2 = r - m;
    int L[n1], R[n2];
    
    for(i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for(j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];
    
    i = j = 0;
    k = l;
    while(i < n1 && j < n2)
    {
        if(L[i] <= R[j]){
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    while(i < n1)
    {
        arr[k] = L[i];
        i++;
        k++;
    }
    
    while(j < n2){
        arr[k] = R[j];
        j++;
        k++;
    }
}

void mergeSort(int arr[], int l, int r)
{
    if(l < r){
        int m = l + (r - l) / 2;
        mergeSort(arr, l, m);
        mergeSort(arr, m+1, r);
        merge(arr, l, m, r);
    }
}

void printArray(int A[], int size)
{
    int i;
    for (i = 0; i < size; i++)
        printf("%d ", A[i]);
    printf("\n");
}

int main()
{
    int arr[] = {12, 11, 13, 5, 6, 7};
    int arr_size = sizeof(arr) / sizeof(arr[0]);

    printf("Given array is \n");
    printArray(arr, arr_size);

    mergeSort(arr, 0, arr_size - 1);

    printf("\nSorted array is \n");
    printArray(arr, arr_size);
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

堆排序

堆排序是基于二叉堆数据结构实现的排序技术。它和选择排序类似先选择最大的元素，把最大的元素放在最后，然后对剩下的元素做重复的过程。 什么是二叉堆(Binary Heap)呢？ 二叉堆是一种二叉树，它具有以下特性：

它是一棵完全树（所有层都是满的，除了最后一层，并且最后一层的结点至少都有左孩子）。这个属性使得二叉堆可以用数组来存储。
二叉堆既不是最小堆也不是最大对。在最小二叉堆中，根节点的值必须是二叉堆中最小的，这个属性对所有结点都是一样的。最大二叉堆和最小二叉堆类似。

最小的的例子：

            10                      10
         /      \               /       \  
       20        100          15         30  
      /                      /  \        /  \
    30                     40    50    100   40

1
2
3
4
5

堆排序算法升序排序

用输入数据建立最大堆，
此时，最大的元素在堆的根节点。将根节点和堆的最后一个元素交换，同时堆的大小减一。对堆进行调整。
当堆的大小大于1时重复1-2步骤。

Implementation

/**
 * 堆排序
 */

#include <stdio.h>

void swap(int *a, int *b)
{
    int t = *a;
    *a = *b;
    *b = t;
}

/**
 * 对堆从上到下进行调整
 */ 
void heapify(int arr[], int n, int i)
{
    int largest = i;
    int l = 2 * i + 1;
    int r = 2 * i + 2;

    if(l < n && arr[l] > arr[largest])
        largest = l;
    if(r < n && arr[r] > arr[largest])
        largest = r;
    if(largest != i)
    {
        swap(&arr[i], &arr[largest]);

        heapify(arr, n, largest);
    }
}

/**
 * 堆排序函数
 */
void heapSort(int arr[], int n)
{
    for(int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i); // 从最后一个元素开始到第一个元素调整堆

    for(int i = n - 1; i >= 0; i--)
    {
        swap(&arr[0], &arr[i]); // 交换最后一个元素和根节点元素
        heapify(arr, i, 0);     // 堆的大小减一，并重新对堆进行调整
    }
}

void printArray(int arr[], int n) 
{ 
    for (int i=0; i<n; ++i) 
        printf("%d\t", arr[i]);
    printf("\n");
}

int main()
{
    int arr[] = {12, 11, 13, 5, 6, 7};
    int n = sizeof(arr) / sizeof(arr[0]);

    heapSort(arr, n);

    printf("Sorted array is \n");
    printArray(arr, n);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

快速排序

和归并排序一样，快速排序也是一种分而治之的算法。它先选择一个元素作为支点(pivot)，以该支点将给定的数组分隔开。不同版本的快速排序方法在选择支点的方法上有所不同：

总是选择第一个元素作为支点
总是选择最后一个元素作为支点
随机选择一个元素作为支点
选择中间的元素作为支点

快速排序的核心过程是分区(partition())。分割的目标是：指定数组和元素x最为数组的支点，把所有比x小的元素放到x的左侧，比它大的元素放到其右侧。在线性的时间内完成这个过程。

选择最后一个元素作为支点，快速排序的示意图如下：

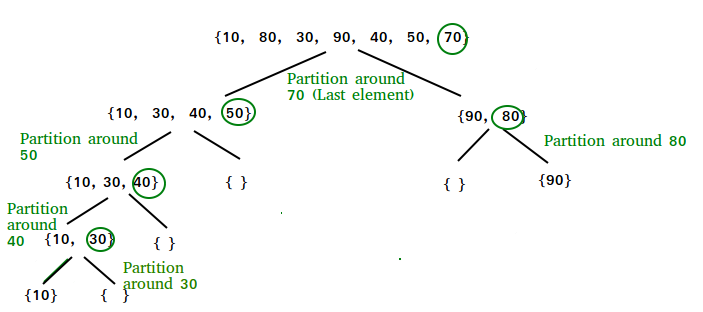
QUICK SORT

Implementation

/**
 * 快速排序
 */
 #include <stdio.h>
void swap(int* a, int* b)
{
    int t = *a;
    *a = *b;
    *b = t;
}

int partition(int arr[], int low, int high)
{
    int pivot = arr[high]; // 支点
    int i = low; // 较大的元素的索引

    for(int j = low; j <= high - 1; j++)
    {
        if(arr[j] <= pivot){
            swap(&arr[i], &arr[j]);
            i++;
        }
    }
    swap(&arr[i], &arr[high]);
    return i;
}



void quickSort(int arr[], int low, int high)
{
    if(low < high){
        int pi = partition(arr, low, high);
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

void printArray(int arr[], int size)
{
    int i;
    for (i=0; i < size; i++)
        printf("%d ", arr[i]);
    printf("\n");
}

int main() 
{
    int arr[] = {10, 7, 8, 9, 1, 1, 5, 0};
    int n = sizeof(arr)/sizeof(arr[0]);
    quickSort(arr, 0, n-1);
    printf("Sorted array: ");
    printArray(arr, n);
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

算法分析

快速排序的时间计算公式

T(n) = T(k) + T(n-k-1) + O(n)

前两两项是递归调用的时间，最后一项是分区过程的时间。k是小于支点的元素的个数。快速排序的时间复杂度取决于输入数组和分区策略，有以下三种情况：

最差情况 最差的情况出现在总是选择了最大的或者最小的元素作为支点。假设我们选择最后一个元素作为支点，最坏的情况就是这个数组已经是排好序的了。时间复杂度计算为：O(n²)。
最佳情况 最佳情况出现在每次都选择了中间大小的元素作为支点。时间复杂度为O(nLogn)。
平均情况 在平均分析时，我们需要考虑所有的数组组合并计算它们的时间复杂度。其解也为O(nLogn)。

尽管快速排序的最差情况下时间复杂度为O(n²)，甚至比归并排序和堆排序还要慢，但是在实际应用中，快速排序会更快，因为它的内部循环可以在大多数架构上，对大多数的实际数据，高效排序，

快速排序可以通过改变选择支点的策略来实现不同的方案，因此最坏的情况很少出现。但是，当数据量很大，并且保存在外部存储中时，归并排序一般会认为更快。

快速排序稳定吗？ 默认的实现不稳定，但是任何的排序算法都可以通过考虑对索引进行比较来稳定算法。

什么是3-way快速排序？ 在简单的快速排序算法，我们选择一个元素作为支点，围绕支点将数组分为左半部分和右半部分并递归地进行快速排序。

当考虑到数组有许多重复的元素时，比如：{1, 4, 2, 4, 2, 4, 1, 2, 4, 1, 2, 2, 2, 2, 4, 1, 4, 4, 4}。如果我们选择4作为支点，用简单的快速排序算法排序时，我们只固定了一个4，然后对剩余的元素递归排序，在3-way快速排序中，数组被分为3部分，小于支点的，等于支点的，大于支点的。实现可以参考这里。

如何在链表中实现快速排序

如何实现迭代快排？

/* arr[] --> Array to be sorted,  
   l  --> Starting index,  
   h  --> Ending index */
void quickSortIterative (int arr[], int l, int h) 
{ 
    // Create an auxiliary stack 
    int stack[ h - l + 1 ]; 
  
    // initialize top of stack 
    int top = -1; 
  
    // push initial values of l and h to stack 
    stack[ ++top ] = l; 
    stack[ ++top ] = h; 
  
    // Keep popping from stack while is not empty 
    while ( top >= 0 ) 
    { 
        // Pop h and l 
        h = stack[ top-- ]; 
        l = stack[ top-- ]; 
  
        // Set pivot element at its correct position 
        // in sorted array 
        int p = partition( arr, l, h ); 
  
        // If there are elements on left side of pivot, 
        // then push left side to stack 
        if ( p-1 > l ) 
        { 
            stack[ ++top ] = l; 
            stack[ ++top ] = p - 1; 
        } 
  
        // If there are elements on right side of pivot, 
        // then push right side to stack 
        if ( p+1 < h ) 
        { 
            stack[ ++top ] = p + 1; 
            stack[ ++top ] = h; 
        } 
    } 
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

参考：迭代快排

快排在数组排序上为何比归并排序好？ 通常的快速排序是一个在位排序（不需要额外的存储空间），而归并排序需要O(N)的空间，N表示数组的大小。内存的分配和释放增加了归并排序的运行时间，比较平均复杂度我们可以发现两种类型的排序都有O(NlogN)的平均复杂度，但是实际中不同，归并排序输在了这而外的存储空间上。

大多数的实际快发的快排实现中使用了随机的版本。随机版本的期望时间复杂度是O(nLogN)。

当对数组排序时，快速排序是一种缓存友好型的排序算法。快排也是尾递归，如何优化尾递归呢？看这里。

归并排序在链表排序上为何比快排好？ 链表和数组的不同主要是在于内存的分配上。和数组不同，链表结点可能不会记录在相邻的内存上。在链表中插入一个元素的时间复杂度是O(1)，空间复杂度也是O(1)。因此归并排序的合并操作对于链表来说不需要额外的空间。

基数排序

基于比较的排序算法的下限是O(NlogN)，它们不可能优于NlogN。计数排序是一种线性排序算法，元素的分布居于1-k，时间复杂度为O(n+k).

假如元素的分布区间是1到n²呢？我们就不能再使用计数排序了，因为时间复杂度已经成了O(n²)了。那我们还怎么在线性时间内对这样的数组排序呢？

答案就是基数排序了！基数排序的思想就是通过一位一位的比较，从低位到高位比较。基数排序算法例子如下：

例子: 原始的没有排序的数组：

170, 45, 75, 90, 802, 24, 2, 66

按低位排序（即个位）: [*注意到 802 在 2的前面, 因为在原始数组中 802 出现在 2 的前面]

170, 90, 802, 2, 24, 45, 75, 66

按下一位排序（即十位）:

802, 2, 24, 45, 66, 170, 75, 90

按最高位排序 (千位) :

2, 24, 45, 66, 75, 90, 170, 802

时间复杂度 基数排序时间复杂度为 O(d*(n+b)) ，d是数组元素的个数，b是数组的进制，如十进制，如果k是元素中的最大值，那么d = O(logb(k))。

Implementation

// C++ implementation of Radix Sort 
#include<iostream> 
using namespace std; 

// A utility function to get maximum value in arr[] 
int getMax(int arr[], int n) 
{ 
	int mx = arr[0]; 
	for (int i = 1; i < n; i++) 
		if (arr[i] > mx) 
			mx = arr[i]; 
	return mx; 
} 

// A function to do counting sort of arr[] according to 
// the digit represented by exp. 
void countSort(int arr[], int n, int exp) 
{ 
	int output[n]; // output array 
	int i, count[10] = {0}; 

	// Store count of occurrences in count[] 
	for (i = 0; i < n; i++) 
		count[ (arr[i]/exp)%10 ]++; 

	// Change count[i] so that count[i] now contains actual 
	// position of this digit in output[] 
	for (i = 1; i < 10; i++) 
		count[i] += count[i - 1]; 

	// Build the output array 
	for (i = n - 1; i >= 0; i--) 
	{ 
		output[count[ (arr[i]/exp)%10 ] - 1] = arr[i]; 
		count[ (arr[i]/exp)%10 ]--; 
	} 

	// Copy the output array to arr[], so that arr[] now 
	// contains sorted numbers according to current digit 
	for (i = 0; i < n; i++) 
		arr[i] = output[i]; 
} 

// The main function to that sorts arr[] of size n using 
// Radix Sort 
void radixsort(int arr[], int n) 
{ 
	// Find the maximum number to know number of digits 
	int m = getMax(arr, n); 

	// Do counting sort for every digit. Note that instead 
	// of passing digit number, exp is passed. exp is 10^i 
	// where i is current digit number 
	for (int exp = 1; m/exp > 0; exp *= 10) 
		countSort(arr, n, exp); 
} 

// A utility function to print an array 
void print(int arr[], int n) 
{ 
	for (int i = 0; i < n; i++) 
		cout << arr[i] << " "; 
} 

// Driver program to test above functions 
int main() 
{ 
	int arr[] = {170, 45, 75, 90, 802, 24, 2, 66}; 
	int n = sizeof(arr)/sizeof(arr[0]); 
	radixsort(arr, n); 
	print(arr, n); 
	return 0; 
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

计数排序

计数排序原理是利用了值分布在一定的范围内。

Implementation

// C++ Program for counting sort 
#include<bits/stdc++.h> 
#include<string.h> 
using namespace std; 
#define RANGE 255 

// The main function that sort 
// the given string arr[] in 
// alphabatical order 
void countSort(char arr[]) 
{ 
	// The output character array 
	// that will have sorted arr 
	char output[strlen(arr)]; 

	// Create a count array to store count of inidividul 
	// characters and initialize count array as 0 
	int count[RANGE + 1], i; 
	memset(count, 0, sizeof(count)); 

	// Store count of each character 
	for(i = 0; arr[i]; ++i) 
		++count[arr[i]]; 

	// Change count[i] so that count[i] now contains actual 
	// position of this character in output array 
	for (i = 1; i <= RANGE; ++i) 
		count[i] += count[i-1]; 

	// Build the output character array 
	for (i = 0; arr[i]; ++i) 
	{ 
		output[count[arr[i]]-1] = arr[i]; 
		--count[arr[i]]; 
	} 

	/* 
	For Stable algorithm 
	for (i = sizeof(arr)-1; i>=0; --i) 
	{ 
		output[count[arr[i]]-1] = arr[i]; 
		--count[arr[i]]; 
	} 
	
	For Logic : See implementation 
	*/

	// Copy the output array to arr, so that arr now 
	// contains sorted characters 
	for (i = 0; arr[i]; ++i) 
		arr[i] = output[i]; 
} 

// Driver code 
int main() 
{ 
	char arr[] = "geeksforgeeks"; 

	countSort(arr); 

	cout<< "Sorted character array is " << arr; 
	return 0; 
} 

// This code is contributed by rathbhupendra

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

参考：这里

桶排序

桶排序非常适用于输入数据非均匀的分布在一定的区域内。比如对0和1.0之间的浮点数进行排序，这些浮点数都是非均匀分布的。

bucketSort(arr[], n)
1) Create n empty buckets (Or lists).
2) Do following for every array element arr[i].
.......a) Insert arr[i] into bucket[n*array[i]]
3) Sort individual buckets using insertion sort.
4) Concatenate all sorted buckets.

1
2
3
4
5
6

桶排序

Implementation

// C++ program to sort an array using bucket sort 
#include <iostream> 
#include <algorithm> 
#include <vector> 
using namespace std; 

// Function to sort arr[] of size n using bucket sort 
void bucketSort(float arr[], int n) 
{ 
	// 1) Create n empty buckets 
	vector<float> b[n]; 
	
	// 2) Put array elements in different buckets 
	for (int i=0; i<n; i++) 
	{ 
	int bi = n*arr[i]; // Index in bucket 
	b[bi].push_back(arr[i]); 
	} 

	// 3) Sort individual buckets 
	for (int i=0; i<n; i++) 
	sort(b[i].begin(), b[i].end()); 

	// 4) Concatenate all buckets into arr[] 
	int index = 0; 
	for (int i = 0; i < n; i++) 
		for (int j = 0; j < b[i].size(); j++) 
		arr[index++] = b[i][j]; 
} 

/* Driver program to test above funtion */
int main() 
{ 
	float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434}; 
	int n = sizeof(arr)/sizeof(arr[0]); 
	bucketSort(arr, n); 

	cout << "Sorted array is \n"; 
	for (int i=0; i<n; i++) 
	cout << arr[i] << " "; 
	return 0; 
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

希尔排序

希尔排序是插入排序的一种变体。在插入排序中，我们将元素只向前移动一个位置。当一个元素需要向前移动很多次时，就需要多次的操作。希尔排序的思想是允许和后面的元素交换。过程如下图所示：

希尔排序

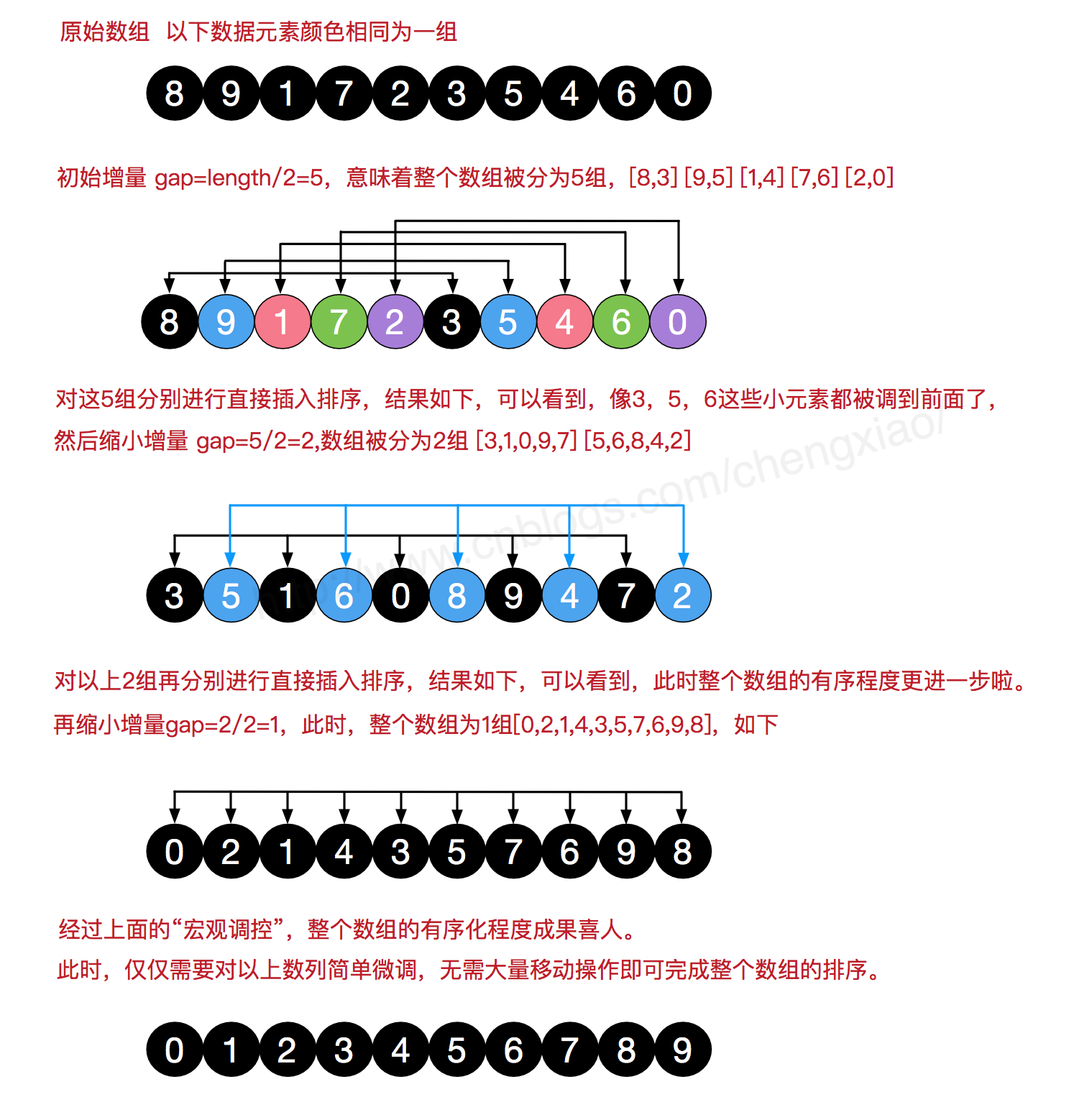
图片来源：链接

Implementation

// C++ implementation of Shell Sort 
#include <iostream> 
using namespace std; 

/* function to sort arr using shellSort */
int shellSort(int arr[], int n) 
{ 
	// Start with a big gap, then reduce the gap 
	for (int gap = n/2; gap > 0; gap /= 2) 
	{ 
		// Do a gapped insertion sort for this gap size. 
		// The first gap elements a[0..gap-1] are already in gapped order 
		// keep adding one more element until the entire array is 
		// gap sorted 
		for (int i = gap; i < n; i += 1) 
		{ 
			// add a[i] to the elements that have been gap sorted 
			// save a[i] in temp and make a hole at position i 
			int temp = arr[i]; 

			// shift earlier gap-sorted elements up until the correct 
			// location for a[i] is found 
			int j;			 
			for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) 
				arr[j] = arr[j - gap]; 
			
			// put temp (the original a[i]) in its correct location 
			arr[j] = temp; 
		} 
	} 
	return 0; 
} 

void printArray(int arr[], int n) 
{ 
	for (int i=0; i<n; i++) 
		cout << arr[i] << " "; 
} 

int main() 
{ 
	int arr[] = {12, 34, 54, 2, 3}, i; 
	int n = sizeof(arr)/sizeof(arr[0]); 

	cout << "Array before sorting: \n"; 
	printArray(arr, n); 

	shellSort(arr, n); 

	cout << "\nArray after sorting: \n"; 
	printArray(arr, n); 

	return 0; 
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

梳子排序

梳子排序是冒泡排序的优化版本。冒泡排序总是比较临近的元素。梳子排序通过大于1的gap优化冒泡排序，gap从一个大的值，每次迭代时缩减，直至值为1，缩减因子为1.3Source: Wiki。

Implementation

// C++ implementation of Comb Sort 
#include<bits/stdc++.h> 
using namespace std; 

// To find gap between elements 
int getNextGap(int gap) 
{ 
	// Shrink gap by Shrink factor 
	gap = (gap*10)/13; 

	if (gap < 1) 
		return 1; 
	return gap; 
} 

// Function to sort a[0..n-1] using Comb Sort 
void combSort(int a[], int n) 
{ 
	// Initialize gap 
	int gap = n; 

	// Initialize swapped as true to make sure that 
	// loop runs 
	bool swapped = true; 

	// Keep running while gap is more than 1 and last 
	// iteration caused a swap 
	while (gap != 1 || swapped == true) 
	{ 
		// Find next gap 
		gap = getNextGap(gap); 

		// Initialize swapped as false so that we can 
		// check if swap happened or not 
		swapped = false; 

		// Compare all elements with current gap 
		for (int i=0; i<n-gap; i++) 
		{ 
			if (a[i] > a[i+gap]) 
			{ 
				swap(a[i], a[i+gap]); 
				swapped = true; 
			} 
		} 
	} 
} 

// Driver program 
int main() 
{ 
	int a[] = {8, 4, 1, 56, 3, -44, 23, -6, 28, 0}; 
	int n = sizeof(a)/sizeof(a[0]); 

	combSort(a, n); 

	printf("Sorted array: \n"); 
	for (int i=0; i<n; i++) 
		printf("%d ", a[i]); 

	return 0; 
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

# 搜索和排序

# 搜索

# 线性搜索

# 二分搜索

# 跳跃搜索

# 插值搜索

# 排序

# 选择排序

# 冒泡排序

# 插入排序

# 归并排序

# 堆排序

# 快速排序

# 基数排序

# 计数排序

# 桶排序

# 希尔排序

# 梳子排序

搜索和排序

搜索

线性搜索

二分搜索

跳跃搜索

插值搜索

排序

选择排序

冒泡排序

插入排序

归并排序

堆排序

快速排序

基数排序

计数排序

桶排序

希尔排序

梳子排序